An article in Scientific American introduces an interesting game theoretic puzzle, the Travelers Dilemma, and proceeds to spin some truly bizarre political conclusions from it. First, the puzzle. Since the effect of the little accompanying story, to judge by the comments at Digg, is primarily to induce people who don’t understand game theory to say lots of profoundly inane things, I’m going to skip it and just sum up the numbers.
You and another player each simultaneously pick a number between 2 and 100 inclusive. The person who picked the lower number (L) gets the payoff (L + 2). The other player gets the payoff (L – 2). If they pick the same number, that’s the payoff for both. The “dilemma” is that the pure strategy Nash Equilibrium for the game is (2, 2), because each bid is dominated by the next smallest number, and backwards induction turns this into a death spiral. Intuitively, it seems like there ought to be a mixed strategy equilibrium, but it’s been years since I had formal game theory training, and I’m not inclined to do much math at the beach, so I’m going to assume there isn’t or the SA piece would’ve mentioned it.
Now, as it turns out, most players—even trained game theorists—don’t follow the zipline of logic to its mutually self-defeating conclusion, and instead pick a number in the mid-90s. This just seems to suggest that there are any number of formal conceptions of “rationality” that, depending on the situation, have some claim to model “rationality” in the normative sense. This is at least one way to read Newcomb’s paradox: As highlighting a tension between a Bayesian decision process and one that proceeds by the elimination of dominated strategies. Just at a first pass, it seems like you could use standard game theory to model the choice between approaches or meta-strategies to the Traveler’s Dilemma—standard backwards induction on the one hand, a fuzzy “pick some high number” strategy on the other:
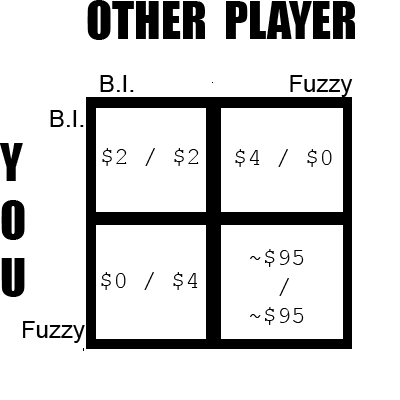
Of course, maybe this just reproduces the original problem when it comes to specifying a range for the fuzzy strategy, but again, disinclined to do the math at the beach.
Anyway, all that’s neither here nor there. What’s really bizarre is that the author, Cornell economist Kaushik Basu, seems to take this as an explosion of the “libertarian presumption” that individuals allowed to freely and rationally pursue their interests will generate good collective outcomes. First, as Jason Kuznicki notes, there’s a hell of a lot of air between this sort of jiggered up formal example and real-world situations in which people have all sorts of ways of ensuring collaboration. The Prisoner’s Dilemma, after all, is also an example of this sort, but it’s well understood that in iterated games over time, much more common in real life, people can arrive at collaborative solutions. More to the point, what Basu finds is precisely that while formal decision theory predicts this sort of perverse outcome, actual people reason in ways that avoid that trap even in the one-shot game. Now, I’m not be especially persuaded that findings from behavioral economics demonstrating systematic cognitive biases away from rational optima establish a strong case for un-libertarian interventions. I do, however, understand why one might think that constitutes a case for such intervention. But I’m damned if I can see how deviations from the predictions of formal decision theory that lead people to collectively superior outcomes are supposed to constitute such a case. If anything, this seems to dovetail with Vernon Smith’s experiments showing that actual economic actors manage to find efficient outcomes even in the absence of conditions the formal models regard as prerequisites.


11 responses so far ↓
1 Blar // May 31, 2007 at 11:29 am
I think the problem with a mixed strategy is that you can induct downward from the highest possible bid in your strategy, moving all of that probability onto the next smallest number. For instance the uniform mixed strategy, p=1/99 for each number, is dominated by p=1/99 for 2-98, p=2/99 for 99, and p=0 for 100.
Even though the design of the game is rather different, this dilemma reminds me of an iterated PD with a specified number of rounds. In that case the (game theory) “rational” thing to do is to always defect, since you can induct back from mutual defection on the last round. But in both cases real people don’t go through the whole backwards induction, so they avoid the death spiral and make more money through their “irrationality.”
2 Glen Whitman // May 31, 2007 at 3:46 pm
As I recall, you can’t get a mixed-strategy equilibrium without having at least two pure-strategy equilibia (as in the sides-of-the-road game) or no pure-strategy equilibrium (as in the matching pennies game).
3 Julian Elson // May 31, 2007 at 4:57 pm
It’s a bit like a Keynesian beauty contest. (The one where whoever guesses closest to 2/3rds of the mean of all participants gets the prize). The Nash equilibrium is zero — but that requires not just that the participants be rational, but that all of them assume that all of the others are rational as well. Moreover, in this case, the rewards for guessing high are very high. If you get about 95 for a high guess or 4 for a guess of 2, then you have to be 96% sure that the other person will also be playing pure strategy Nash for it to be worthwhile, assuming risk neutrality.
4 Michael B Sullivan // May 31, 2007 at 6:38 pm
Yeah, I think that the TD is kind of rigged. If you choose $2, you are assuming that you will get at most $4, and probably $2 (since you got to the “bidding $2” strategy by assuming that your opponent will think that $2 is the right bid). If you bid higher than $2, then you stand to lose $2 from your outcome (you could get $0, if your opponent really did bid $2), and up to $98 higher. As Julian Elson says, you have to be AWFULLY sure that your opponent is going to bid $2 before giving up a chance at $100 for a guaranteed $2 sounds like a good idea.
Moreover, I think that if you have actual humans play the game, they’re going to have a thought process that says, “$2 is approximately equal to $0, so who cares?” I know you’re not supposed to think about that in game theory — $2 is supposed to be $2 — but seriously, if you’re playing at those stakes, who the hell cares about $2? Also, if you choose $100 and your opponent chooses $99, who the hell cares if you get $97 and he gets $101? You wouldn’t try to screw him by bidding $98 because, to a human, the $97 that you get via bidding $100 and the $100 that you get by bidding $98 are functionally equivalent.
I think that a more interesting variation of the traveller’s dilemma would be “choose a number between $20 and $100, and I’ll pay you the lower of the two values, +/- $20.” At that point, I think, people might actually get worried about the differential. If the difference between a $100/$99 and a $100/$100 bid isn’t $3 bucks for the “loser,” but $21, then you might see humans behaving considerably more like the rational model predicts.
If I’m right that $20 swings would make people behave more like the rational model, then all the TD is saying above is that $2 swings are below the level of resolution that humans really perceive.
5 thoreau // May 31, 2007 at 7:23 pm
Amusingly unfortunate fact: The author of that article is the Carl Marks Chair in International Studies at Cornell.
Yes, I spelled that name correctly (or at least the way it’s spelled in his bio in the article). Must suck to be an economist who has to say “I’d like to thank Carl Marks for endowing my academic chair.”
6 Dave W. // Jun 1, 2007 at 11:31 am
My theory:
I think that whether the death spiral is actually engaged by real people is primarily sensitive to a number I call the “loser ratio.” Let me explain:
In the example of the article, the max payout is nominally 100 and the difference between the winner and the loser is nominally 4. The “loser ratio” is therefore 4/100 or 4%. At a loser ratio of 4%, I do not think people engage the death spiral.
Now lets say that max payout was reduced to 10, but the difference between winner and loser remained at 4. This “loser ratio” would be 40%. Even at this loser ratio, I think most people would tend not to engage the death spiral and that bids of 10 would be most common.
I think once the “loser ratio” above 50%, however, people will engage the death spiral. In other words, say the max payout was reduced to 6, and the win/lose differential remained at 4. Then the “loser ratio” would become 67% and I think people would tend to engage the spiral and bid it down to 2 quite reliable.
The place only case where I think people would bid substantially between the min and the max is when the “loser ratio” is 50%. In other words, if the max payout were 8, and the win/loss diff remained at 4, then I think you might see people bidding 4 or 5 (instead of the min 2 or the max 8).
I don’t know why I think it is all about this construct of the “loser ratio,” but I am pretty sure it is. Maybe Nash can explain why now that he is not crazee anymore.
7 Dave W. // Jun 1, 2007 at 11:47 am
Or, to stick with the max payout of 100, if the +/- is +20/-20 for a win/loss diff of 40, I think bids of 100 would still be the most common.
If the max payout remained 100, but the reward/penalty were increased to +25/-25, then I think bids of around 50 would happen.
Once the reward / penalty goes above +25/-25, then I think the bidding would, in fact, go down the death spiral to 2, even for real flesh’n’blood persons.
8 Joel // Jun 1, 2007 at 4:59 pm
Blar has the right idea why you can’t get a mixed strategy equilibrium in this game.
Glen’s point “you can’t get a mixed-strategy equilibrium without having at least two pure-strategy equilibia (as in the sides-of-the-road game) or no pure-strategy equilibrium (as in the matching pennies game).” isn’t always true.
You can definitely have one pure strategy equilibrium and two (or some other even number of) mixed strategy equilibria.
9 Michael B Sullivan // Jun 2, 2007 at 2:12 pm
Dave: I suspect that the amount of money that one would quibble over is a function of both the amount of money riding on this transaction, and the size of transactions that you’re used to dealing with. So, for example, if we were talking about a young kid, who generally deals in very small amounts of money, they might be interested in trying to maximize their $3 swings in the TD. Most adults would not. If you reduced the stakes to $10, and kept the swing at +/-$2, I agree that the odds that people would care much would increase.
The way I see it, $20 starts to be a “real” amount of money for most adults, and so they may care to try to maximize blocks of $20 that they get, even in a relatively large transaction.
10 Dave W. // Jun 3, 2007 at 8:52 pm
It would be cool to have a study to see which of our respective hypotheses is correct, Michael.
Obviously, there would be some spread, or perhaps interpolation between, bid max, bid half and bid min, but I still think there would be three bid peaks and it would cut across kid versus adult, smart versus dumb and rich versus poor.
I wouldn’t be shocked if you were correct, but, absent empirical evidence, I don’t think you are. I think it is all about the “loser ratio” and whether the loser ratio is over 50%, under 50% or at approximately 50%.
11 X. Trapnel // Jun 4, 2007 at 5:12 pm
The SciAm article mentions (or maybe just links to) studies that change around the numbers, fyi.
“[Nash] requires not just that the participants be rational, but that all of them assume that all of the others are rational as well” — it requires more than this. There is nothing irrational about my expecting my perfectly rational partner to pick a non-Nash strategy, and reacting appropriately, while she expects me to pick a non-Nash strategy (different than the one I pick), and best-responds to that (with something I didn’t expect). It’s not *stable*, but so what? Rationalizability, not Nash, is all rationality really guarantees.